OSSE SCHAAKVERENIGING - OSV

Tijdens de vierde ronde van het Open Osse Schaakkampioenschap (28 april 2015) was ik getuige van het eindspel KRK. Dit is de internationale notatie voor een eindspel met de witte koning plus een toren (Engels rook) tegen de zwarte koning. Beide spelers hadden nog slechts een paar minuten op de klok voor het vallen van de vlag. Alhoewel dit eindspel theoretisch voor wit is gewonnen speelde de zwartspeler door met het idee dat wit maar moest bewijzen hem binnen de tijd mat te zetten. De witspeler bleek duidelijk niet op de hoogte hoe dit eindspel tot een goed einde te brengen en verdeed zijn tijd met nutteloze zetten waarna wit’s vlag viel. Gelukkig voor wit nog remise: zwart heeft geen matpotentieel. Na afloop liet een ervaren clubschaker zien hoe dit eindspel wel te spelen.

Als liefhebber van eindspel databases heb ik me verdiept in de vraag of we wat kunnen leren over de aanpak van eindspelen op grond van de kennis opgeborgen in de eindspel databases.

Om te beginnen iets over de vorderingen die recent op dit gebied zijn gemaakt. Tot voor kort zijn de Naiimov tablebases het meest gebruikelijk. Een eindspel database wordt in vakjargon “tablebase” genoemd meestal voorafgegaan door de naam van de uitvinder. De 5-stukken Naiimov tablebase (uitgekomen in 1998) is qua grootte nog net te behappen op een normale PC (7 GB). Voor 6-stukken (uitgekomen in 2005) stijgt de grootte exponentieel: 1200 GB. Dit zet je thuis niet meer op je PC. Je kunt deze database wel online raadplegen; op de OSV-website is hiervoor een link aanwezig. In 2013 is een nieuwe vorm van opslag bedacht door Ronald de Man (het zogenaamde Syzygy formaat) die de databases kleiner en sneller maakt: 5-stukken 0,94 GB en 6-stukken 150 GB.

De programmeurs Zakharov and Makhnichev hebben de Lomonosov supercomputer aan de Staatsuniversiteit van Moskou 6 maanden laten rekenen om de 7-stukken database te construeren met een grootte van 140.000 GB (gereed gekomen in april 2013 en vrijgegeven in oktober 2014) gebruikmakend van een nieuw algorithme.

Wat kunnen we als schakers leren van deze databases? Laten we met enkele eenvoudige eindspelen beginnen. In mijn boekenkast staat nog steeds het antieke “Praktische Schaaklessen Tweede Deel” van Den Hertog en Eeuwe uit 1956 waarin een hoofdstuk staat genaamd “Matvoering van de Roi Dépouillé” (Frans: kale, uitgekleedde, naakte koning). Omdat dit boekje uit 1956 is onderzocht ik of deze eindspelkennis door de databases is achterhaald of verbeterd. Het antwoord is kort: nee. De regels voor de snelste matvoering zoals beschreven in het boekje uit 1956 zie je terug als je het eindspel met behulp van de database naspeelt. Grappig is de discussie over het minimaal aantal benodigde zetten voor mat in KQK. Euwe zegt 9 met de opmerking dat sommige theoretici 10 beweren. Euwe laat zien dat het toch echt in 9 kan. De eindspel database KQK toont aan dat je voor onderstaande stelling (Diagram 1) minimaal 10 zetten nodig hebt om zwart mat te zetten bij optimaal tegenspel.

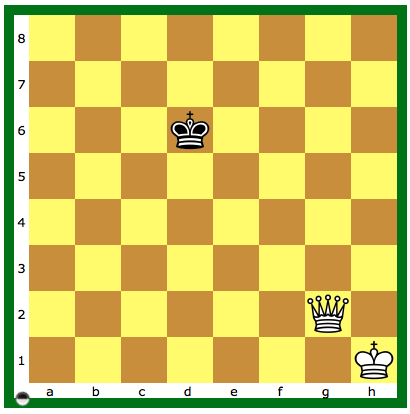Diagram 1: Wit aan zet; mat-in-10

Voor het eindspel KRK zijn minimaal 16 zetten nodig en voor KBBK (koning+2 lopers tegen koning) 19 zetten (in 1956 dacht men nog 18).

Voor bovengenoemde eindspelen zijn logische regels, richtlijnen of strategieën te beschrijven waarmee een schaker uit de voeten kan om binnen een redelijk aantal zetten (misschien niet altijd de meest optimale) de kale koning mat te zetten. Bedenk wel dat het matzetten binnen 50 zetten moet gebeuren. Als er namelijk 50 zetten lang geen stuk wordt geslagen of pion wordt verzet is het remise (de 50-zetten regel).

Zoals ieder schaker weet is het eindspel KBNK (koning+loper+paard tegen koning) buitengewoon lastig. In mijn boekje uit 1956 was het nog niet bekend hoeveel zetten voor mat nodig waren. Nu weten we uit de KBNK database dat dit er 33 zijn. Er bestaan vele ingewikkelde richtlijnen en regels die pagina’s vol vullen om dit eindspel tot een goed einde te brengen. Euwe wijdt er maar liefst 13 pagina’s aan. In de praktijk zal zelfs een ervaren schaker de zwarte koning binnen 50 zetten niet mat krijgen met weinig tijd op de klok zodat remise het resultaat zal zijn.

Vanuit onderstaande stelling (Diagram 2) zegt Euwe 18 zetten nodig te hebben voor mat.

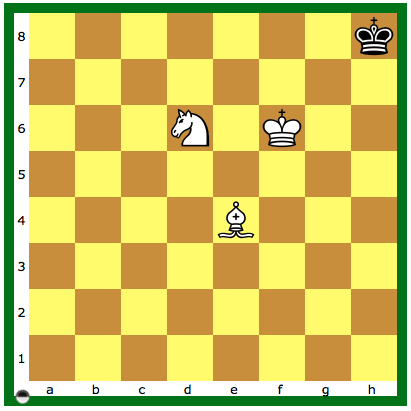Diagram 2: Wit aan zet; mat-in-20

De database leert echter dat er 20 nodig zijn bij optimaal tegenspel van zwart. Speel de volgende zettenreeks eens na (dit is slechts één van de vele varianten):

1.Pf7+ Kg8 2.Ld3 Kf8 3.Lh7 Ke8 4.Pe5 Kd8 5.Le4 Kc7 6.Pc4 Kd7 7.Kf7 Kd8 8.Lc6 Kc7 9.Lb5 Kd8 10.La4 Kc7 11.Ke6 Kc8 12.Kd6 Kd8 13.Pa5 Kc8 14.Ld7+ Kb8 15.Kc6 Ka7 16.Lc8 Kb8 17.Kd7 Ka7 18.Kc7 Ka8 19.Lb7+ Ka7 20.Pc6#

Klik	om deze zetten op de pgn-viewer na te spelen.

Het is lastig de logica van iedere zet werkelijk te begrijpen. Toch is dit de snelste manier om de zwarte koning mat te zetten.

Voor het eindspel KPK (koning+pion tegen koning) vinden we een aantal duidelijke regels in de schaakleerboeken, bijvoorbeeld de vierkant-regel en het oppositie-principe. Vóór het bestaan van eindspel databases waren deze regels al lang bekend. De KPK database leert ons niets nieuws. Ook voor een eindspel met meerdere pionnen is de logica achter de zetten in de database voor een schaker goed te begrijpen.

Maar hoe zit dat nu met de 6- en 7-stukken databases? Allereerst hebben we bizarre stellingen die in de praktijk nooit zullen voorkomen en alleen voor theoretici interessant zijn. Zie bijvoorbeeld het 7-stukken eindspel in Diagram 3:

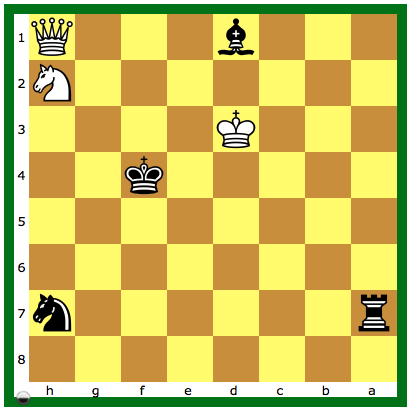Diagram 3: Zwart aan zet; mat-in-545

Maar er zijn ook stellingen die we wel in de praktijk zouden kunnen tegenkomen zoals onderstaande stelling (Stiller, Karrer, Thompson, 2000):

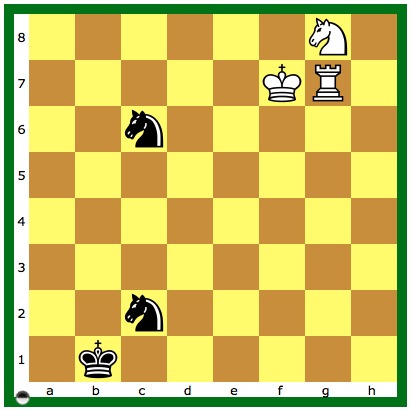Diagram 4: Wit aan zet; mat-in-262

In de speelpraktijk is deze stelling remise wegens de 50-zetten regel. Bovendien is er geen speler ter wereld die zwart hier mat krijgt (aangenomen dat zwart geen fouten maakt). Tim Krabbé zegt er het volgende van:

A grandmaster wouldn't be better at these endgames than someone who had learned chess yesterday. It's a sort of chess that has nothing to do with chess, a chess that we could never have imagined without computers. The Stiller moves are awesome, almost scary, because you know they are the truth, God's Algorithm – it's like being revealed the Meaning of Life, but you don't understand one word.

Zelfs een grootmeester ontgaat de logica van de zetten volkomen. We weten dat het steeds de beste zetten zijn maar waarom? Ook is er geen enkele regel of strategie uit de zettenreeks af te leiden die een schaker kan helpen bij het tot winst voeren van een vergelijkbare stelling. Kortom: voor de schaakpraktijk levert de database in dit geval geen inzicht op hoe een dergelijk eindspel moet worden aangepakt. Deze stelling is te moeilijk om te worden begrepen door het menselijk brein.

Natuurlijk zijn er ook 6- en 7-stukken eindspelen die meer in de prakrijk zullen voorkomen dan bovenstaand voorbeeld. En ook al kunnen we niet altijd de logica van alle zetten doorgronden in ieder geval geeft de database uitsluitsel of een stelling winst, verlies of remise is. Ook voor eindspelstudies bewijzen de databases hun diensten. In menige eindspelstudie zijn al fouten gevonden dankzij de database kennis. Nu kan de eindspelcomponist alvorens zijn studie te publiceren eerst de database erop loslaten om te controleren of zijn oplossing correct is.

Magnus Carlsen zei in 2013: “I don’t think we’ll see seven pieces resolved in our lifetime.” En zie wat is gebeurd. Men heeft becijferd dat er 10 jaar nodig is om de database met één stuk uit te breiden. Dus over 250 jaar is er een 32-stukken database en is het schaakspel opgelost. De wereld zal dan weten of wit altijd kan winnen als beide spelers de beste zetten doen. Het is aardig om te vermelden dat er een aantal Arabische oliesjeiks bereid is het project te sponsoren om de complete database in 2263 klaar te hebben. Het is misschien een troost voor ons OSV-leden dat we dit niet meer meemaken.

Oss, 6 mei 2015
Cees Timmer